ESTRUCTURAS DE DATOS: ÁRBOLES

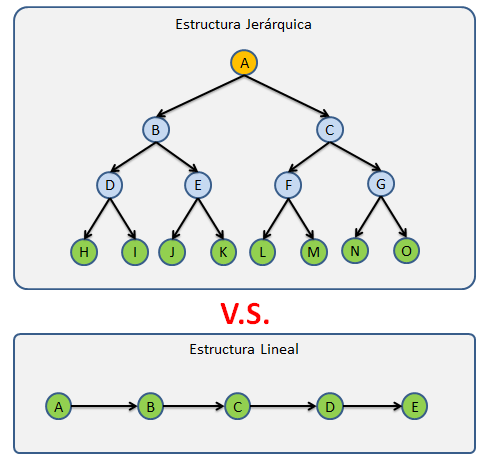
Los Árboles son las estructuras de datos más utilizadas, pero también una de las más complejas, Los Árboles se caracterizan por almacenar sus nodos en forma jerárquica y no en forma lineal como las listas ligadas, colas, pilas, etc., de las cuales ya hemos hablado en días pasados.

 

 Datos importantes de los Árboles

Para comprender mejor que es un árbol comenzaremos explicando cómo está estructurado.

Nodos: Se le llama Nodo a cada elemento que contiene un Árbol.

Nodo Raíz: Se refiere al primer nodo de un Árbol, Solo un nodo del Árbol puede ser la Raíz.

Nodo Padre: Se utiliza este término para llamar a todos aquellos nodos que tiene al menos un hijo.

Nodo Hijo: Los hijos son todos aquellos nodos que tiene un padre.

Nodo Hermano: Los nodos hermanos son aquellos nodos que comparte a un mismo padre en común dentro de la estructura.

Nodo Hoja: Son todos aquellos nodos que no tienen hijos, los cuales siempre se encuentran en los extremos de la estructura.

Nodo Rama: Estos son todos aquellos nodos que no son la raíz y que además tiene al menos un hijo.

 

Los arboles a demás de los nodos tiene otras propiedades importantes que son utilizadas en diferentes ámbitos los cuales son:

Nivel: Nos referimos como nivel a cada generación dentro del árbol. Por ejemplo, cuando a un nodo hoja le agregamos un hijo, el nodo hoja pasa a ser un nodo rama, pero además el árbol crece una generación por lo que el Árbol tiene un nivel mas. Cada generación tiene un número de Nivel distinto que las demás generaciones.

• Un árbol vacío tiene 0 niveles
• El nivel de la Raíz es 1
• El nivel de cada nodo se calculado contando cuantos nodos existen sobre el, hasta llegar a la raíz + 1, y de forma inversa también se podría, contar cuantos nodos existes desde la raíz hasta el nodo buscado + 1.

  Altura: Le llamamos Altura al número máximo de niveles de un Árbol.

 

 

La altura es calculada mediante recursividad tomando el nivel mas grande de los dos sub-árboles de forma recursiva de la siguiente manera:

altura = max(altura(hijo1), altura(hijo2), altura(hijoN)) + 1

Peso: Conocemos como peso a el número de nodos que tiene un Árbol. Este factor es importante porque nos da una idea del tamaño del árbol y el tamaño en memoria que nos puede ocupar en tiempo de ejecución (Complejidad Espacial en análisis de algoritmos.)

 

 

El peso se puede calcular mediante cualquier tipo de recorrido el cual valla contando los nodos a medida que avanza sobre la estructura. El peso es un árbol es igual a la suma del peso de los sub-árboles hijos + 1

peso = peso(hijo1) + peso(hijo2) + peso(hijoN)+ 1

 

Orden: El Orden de un árbol es el número máximo de hijos que puede tener un Nodo.

 

Notemos que un Árbol con Orden = 1 no tendría sentido ya que seria una estructura lineal. 

Este valor no lo calculamos, si no que ya lo debemos conocer cuando diseñamos nuestra estructura, ya que si queremos calcular esto lo que obtendremos es el grado (hablamos de él a continuación).

Grado: El grado se refiere al número mayor de hijos que tiene alguno de los nodos del Árbol y está limitado por el Orden, ya que este indica el número máximo de hijos que puede tener un nodo.

 

El grado se calcula contando de forma recursiva el número de hijos de cada sub-árbol hijo y el número de hijos del nodo actual para tomar el mayor, esta operación se hace de forma recursiva para recorrer todo el árbol.

grado = max(contarHijos(hijo1),contarHijos(hijo2), contarHijos(hijoN), contarHijos(this))

Sub-Árbol: Conocemos como Sub-Árbol a todo Árbol generado a partir de una sección determinada del Árbol, Por lo que podemos decir que un Árbol es un nodo Raíz con N Sub-Árboles.

 Existen escenarios donde podemos sacar un Sub-Árboles del Árbol para procesarlo de forma separada, de esta forma el Sub-Árboles pasa a ser un Árbol independiente, También podemos eliminar Sub-Árboles completos, Agregarlos, entre otras operaciones.

Árbol n-ario

los arboles n-arios son aquellos arboles donde el número máximo de hijos por nodo es de N, en la figura 7 podemos apreciar dos árboles con grado 2 y grado 3, estos dos arboles también los podemos definir como Árbol n-ario con n = 2 y n=3 respectivamente.

Árboles binarios

Esta estructura se caracteriza por que cada nodo solo puede tener máximo 2 hijo, dicho de otra manera, es un Árbol n-ario de Grado 2.

 

 

 

 

Árbol binario lleno: Es aquel que el que todos los nodos tienen cero o 2 hijos con excepción de la Raíz.

 

 

 Árbol binario perfecto: Es un Árbol lleno en donde todos las Hojas están en el mismo Nivel.

 

 

 En la imagen podemos apreciar que el árbol de la izquierda tiene todas sus hojas al mismo nivel y que además está lleno, lo que lo convierte en un árbol binario perfecto. Sin embargo, del lado derecho podemos ver que, aunque el árbol está lleno no tiene todas las hojas al mismo nivel lo que hace que no sea un árbol binario perfecto, pero si lleno.